euclidean_polygons

The category of Euclidean polygons defined in the real plane.

See flatsurf.geometry.categories for a general description of the category framework in sage-flatsurf.

Normally, you won’t create this (or any other) category directly. The correct category of a polygon is automatically determined.

EXAMPLES:

sage: from flatsurf.geometry.categories import EuclideanPolygons
sage: C = EuclideanPolygons(QQ)

sage: from flatsurf import polygons
sage: polygons.square() in C
True

class flatsurf.geometry.categories.euclidean_polygons.EuclideanPolygons(base, name=None)

The category of Euclidean polygons defined in the real plane over a fixed base ring.

EXAMPLES:

sage: from flatsurf.geometry.categories import EuclideanPolygons
sage: EuclideanPolygons(QQ)
Category of euclidean polygons over Rational Field

class Convex(base_category)

The subcategory of convex Euclidean polygons in the real plane.

EXAMPLES:

For historic reasons, there is the shortcut ConvexPolygons to get the Euclidean convex polygons:

sage: from flatsurf import ConvexPolygons
sage: C = ConvexPolygons(QQ)

sage: from flatsurf.geometry.categories import EuclideanPolygons
sage: C is EuclideanPolygons(QQ).Convex().Simple()
True

sage: C(vertices=[(0,0), (2,0), (1,1)])
Polygon(vertices=[(0, 0), (2, 0), (1, 1)])

sage: C(edges=[(1,0), (0,1), (-1,0), (0,-1)])
Polygon(vertices=[(0, 0), (1, 0), (1, 1), (0, 1)])

This axiom can also be created over non-fields:

sage: ConvexPolygons(ZZ)
Category of convex simple euclidean polygons over Integer Ring

class ParentMethods

Provides methods available to all convex Euclidean polygons in the real plane.

If you want to add functionality to such polygons, you probably want to put it here.

is_convex(strict=False)

Return whether this is a convex polygon.

INPUT:

• strict – whether to check for strict convexity, i.e., a polygon with a π angle is not considered convex.

EXAMPLES:

sage: from flatsurf import polygons
sage: S = polygons.square()
sage: S.is_convex()
True
sage: S.is_convex(strict=True)
True

class ParentMethods

Provides methods available to all Euclidean polygons in the real plane.

If you want to add functionality to such polygons, you probably want to put it here.

angle(e, numerical=None, assume_rational=None)

Return the angle at the beginning of the start point of the edge e.

EXAMPLES:

sage: from flatsurf.geometry.polygon import polygons
sage: polygons.square().angle(0)
1/4
sage: polygons.regular_ngon(8).angle(0)
3/8

sage: from flatsurf import Polygon
sage: T = Polygon(vertices=[(0,0), (3,1), (1,5)])
sage: [T.angle(i, numerical=True) for i in range(3)]  # abs tol 1e-13
[0.16737532973071603, 0.22741638234956674, 0.10520828791971722]
sage: sum(T.angle(i, numerical=True) for i in range(3))   # abs tol 1e-13
0.5

angles(numerical=None, assume_rational=None)

Return the list of angles of this polygon (divided by \(2 \pi\)).

EXAMPLES:

sage: from flatsurf import Polygon

sage: T = Polygon(angles=[1, 2, 3])
sage: [T.angle(i) for i in range(3)]
[1/12, 1/6, 1/4]
sage: T.angles()
(1/12, 1/6, 1/4)
sage: sum(T.angle(i) for i in range(3))
1/2

area()

Return the area of this polygon.

EXAMPLES:

sage: from flatsurf.geometry.polygon import polygons
sage: polygons.regular_ngon(8).area()
2*a + 2
sage: _ == 2*AA(2).sqrt() + 2
True

sage: AA(polygons.regular_ngon(11).area())
9.36563990694544?

sage: polygons.square().area()
1
sage: (2*polygons.square()).area()
4

centroid()

Return the coordinates of the centroid of this polygon.

ALGORITHM:

We use the customary formula of the centroid of polygons, see https://en.wikipedia.org/wiki/Centroid#Of_a_polygon

EXAMPLES:

sage: from flatsurf.geometry.polygon import polygons
sage: P = polygons.regular_ngon(4)
sage: P
Polygon(vertices=[(0, 0), (1, 0), (1, 1), (0, 1)])
sage: P.centroid()
(1/2, 1/2)

sage: P = polygons.regular_ngon(8); P
Polygon(vertices=[(0, 0), (1, 0), (1/2*a + 1, 1/2*a), (1/2*a + 1, 1/2*a + 1), (1, a + 1), (0, a + 1), (-1/2*a, 1/2*a + 1), (-1/2*a, 1/2*a)])
sage: P.centroid()
(1/2, 1/2*a + 1/2)

sage: P = polygons.regular_ngon(11)
sage: C = P.centroid()
sage: P = P.translate(-C)
sage: P.centroid()
(0, 0)

edge(i)

Return the vector going from vertex i to the following vertex in counter-clockwise order.

EXAMPLES:

Note that this wraps around if i is negative or exceeds the number of vertices:

sage: from flatsurf import polygons
sage: s = polygons.square()
sage: s.edge(-1)
(0, -1)
sage: s.edge(0)
(1, 0)
sage: s.edge(1)
(0, 1)
sage: s.edge(2)
(-1, 0)
sage: s.edge(3)
(0, -1)
sage: s.edge(4)
(1, 0)

edges()

Return the edges of this polygon as vectors in the plane going from one vertex to the next one.

EXAMPLES:

sage: from flatsurf import polygons
sage: s = polygons.square()
sage: s.edges()
[(1, 0), (0, 1), (-1, 0), (0, -1)]

erase_marked_vertices()

Return a copy of this polygon without marked vertices.

EXAMPLES:

sage: from flatsurf import Polygon
sage: p = Polygon(vertices=[(0, 0), (2, 0), (4, 0), (2, 2)])
sage: p.erase_marked_vertices()
Polygon(vertices=[(0, 0), (4, 0), (2, 2)])

field()

EXAMPLES:

sage: from flatsurf import polygons
sage: S = polygons.square()
sage: S.field()
doctest:warning
...
UserWarning: field() has been deprecated and will be removed from a future version of sage-flatsurf; use base_ring() or base_ring().fraction_field() instead
Rational Field

get_point_position(point, translation=None)

Return the combinatorial classification of a point and a polygon.

INPUT:

• point – a point in the plane as a SageMath vector or pair of numbers

OUTPUT:

a geometry.polygon.PolygonPosition object

ALGORITHM:

We use a winding number algorithm see https://en.wikipedia.org/wiki/Point_in_polygon#Winding_number_algorithm

EXAMPLES:

sage: from flatsurf import polygons, Polygon
sage: S = polygons.square()

sage: S.get_point_position((1/2, 1/2))
point positioned in interior of polygon
sage: S.get_point_position((1, 0))
point positioned on vertex 1 of polygon
sage: S.get_point_position((1, 1/2))
point positioned on interior of edge 1 of polygon
sage: S.get_point_position((1, 3/2))
point positioned outside polygon

sage: p = Polygon(edges=[(1, 0), (1, 0), (1, 0), (0, 1), (-3, 0), (0, -1)])
sage: p.get_point_position([10, 0])
point positioned outside polygon
sage: p.get_point_position([1/2, 0])
point positioned on interior of edge 0 of polygon
sage: p.get_point_position([3/2, 0])
point positioned on interior of edge 1 of polygon
sage: p.get_point_position([2,0])
point positioned on vertex 2 of polygon
sage: p.get_point_position([5/2, 0])
point positioned on interior of edge 2 of polygon
sage: p.get_point_position([5/2, 1/4])
point positioned in interior of polygon

is_convex(strict=False)

Return whether this is a convex polygon.

INPUT:

• strict – whether to check for strict convexity, i.e., a polygon with a π angle is not considered convex.

EXAMPLES:

sage: from flatsurf import polygons
sage: S = polygons.square()
sage: S.is_convex()
True
sage: S.is_convex(strict=True)
True

is_degenerate()

Return whether this polygon is considered degenerate.

This implements flatsurf.geometry.categories.polygons.Polygons.ParentMethods.is_degenerate().

EXAMPLES:

Polygons with zero area are considered degenerate:

sage: from flatsurf import Polygon
sage: p = Polygon(vertices=[(0, 0), (2, 0), (1, 0)], check=False)
sage: p.is_degenerate()
True

Polygons with marked vertices are considered degenerate:

sage: from flatsurf import Polygon
sage: p = Polygon(vertices=[(0, 0), (2, 0), (4, 0), (2, 2)])
sage: p.is_degenerate()
True

is_equiangular()

Return whether all sides of this polygon meet at the same angle.

EXAMPLES:

sage: from flatsurf import Polygon
sage: p = Polygon(vertices=[(0, 0), (2, 0), (2, 2), (0, 2)])
sage: p.is_equiangular()
True

is_equilateral()

Return whether all sides of this polygon have the same length.

EXAMPLES:

sage: from flatsurf import Polygon
sage: p = Polygon(vertices=[(0, 0), (2, 0), (2, 2), (0, 2)])
sage: p.is_equilateral()
True

is_rational()

Return whether this is a rational polygon, i.e., all its angles() are rational multiples of π.

EXAMPLES:

sage: from flatsurf import Polygon
sage: p = Polygon(vertices = [(1, 0), (0, 1), (-1, -1)])
sage: p.is_rational()
False

Note that determining rationality is somewhat costly. Once established, this refines the category of the triangle:

sage: p = Polygon(vertices = [(0, 0), (1, 0), (0, 1)])
sage: p.category()
Category of convex simple euclidean polygons over Rational Field
sage: p.is_rational()
True
sage: p.category()
Category of rational convex simple euclidean polygons over Rational Field

is_simple()

Return whether this is a simple polygon, i.e., without self-intersection.

EXAMPLES:

sage: from flatsurf import polygons sage: s = polygons.square() sage: s.is_simple() True

join(other, edge, other_edge)

Return the polygon obtained by gluing this polygon and other along their edge and other_edge, respectively.

The polygons have to be such that the glued edges are identical but with opposite orientation.

INPUT:

• other – a polygon over the same base ring as this polygon

• edge – an integer; the index of the edge of this polygon along which to glue

• other_edge – an integer; the index of the edge of other along which to glue

EXAMPLES:

sage: from flatsurf import Polygon
sage: P = Polygon(vertices=[(0, 0), (1, 0), (0, 1)])
sage: Q = Polygon(vertices=[(1, 0), (1, 1), (0, 1)])
sage: P.join(Q, 1, 2)
Polygon(vertices=[(0, 0), (1, 0), (1, 1), (0, 1)])

sage: P.join(P, 1, 1)
Traceback (most recent call last):
...
ValueError: glued edges must be identical with opposite orientation

sage: Q = Polygon(vertices=[(0, 0), (0, 1), (-1, 1)])
sage: P.join(Q, 1, 2)
Traceback (most recent call last):
...
ValueError: glued edges must be identical with opposite orientation

sage: P.join(Q, 2, 0)
Polygon(vertices=[(0, 0), (1, 0), (0, 1), (-1, 1)])

Polygons cannot be joined if that would lead to a self-intersecting polygon:

sage: P = Polygon(vertices=[(0, 0), (2, 0), (2, 2), (0, 2), (1, 1)])
sage: Q = Polygon(vertices=[(0, 0), (1, 1), (2, 2), (0, 2)])
sage: P.join(Q, 4, 0)
Traceback (most recent call last):
...
NotImplementedError: polygon self-intersects

module()

Return the free module of rank 2 in which this polygon embeds.

EXAMPLES:

sage: from flatsurf import polygons
sage: S = polygons.square()
sage: S.module()
doctest:warning
...
UserWarning: module() has been deprecated and will be removed in a future version of sage-flatsurf; use base_ring()**2 instead
Vector space of dimension 2 over Rational Field

plot(translation=None, polygon_options={}, edge_options={}, vertex_options={})

Return a plot of this polygon with the origin at translation.

EXAMPLES:

sage: from flatsurf import polygons
sage: S = polygons.square()
sage: S.plot()
...Graphics object consisting of 3 graphics primitives

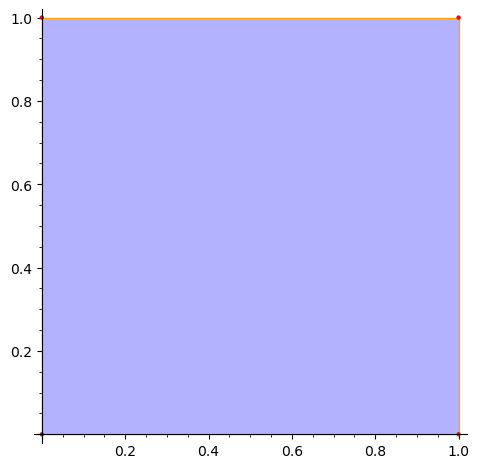
We can specify an explicit zorder to render edges and vertices on top of the axes which are rendered at z-order 3:

sage: S.plot(edge_options={'zorder': 3}, vertex_options={'zorder': 3})
...Graphics object consisting of 3 graphics primitives

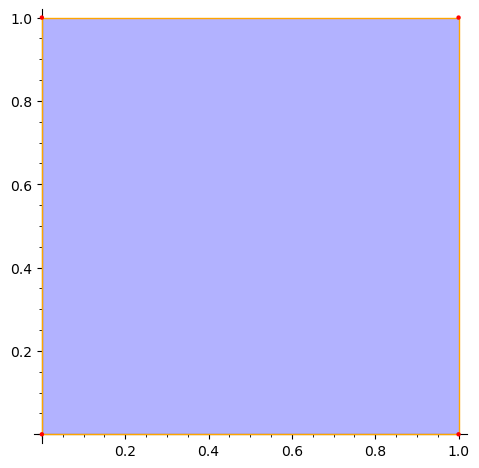
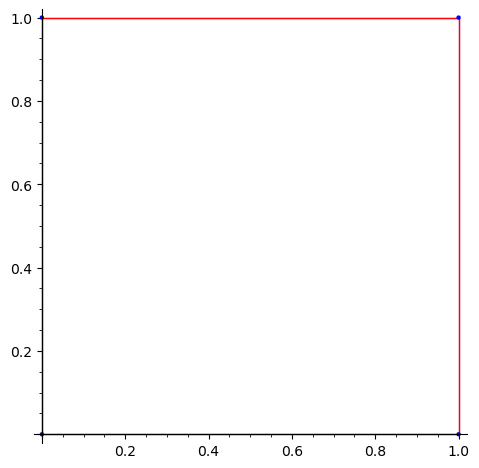
We can control the colors, e.g., we can render transparent polygons, with red edges and blue vertices:

sage: S.plot(polygon_options={'fill': None}, edge_options={'color': 'red'}, vertex_options={'color': 'blue'})
...Graphics object consisting of 3 graphics primitives

slopes(relative=False)

Return the slopes of this polygon as vectors in the plane.

INPUT:

• relative – a boolean (default: False); whether to return the slopes not as absolute vectors parallel to the edges but relative to the previous edge, i.e., after turning the previous edge to be parallel to the x axis.

EXAMPLES:

sage: from flatsurf import polygons
sage: s = polygons.square()
sage: s.slopes()
[(1, 0), (0, 1), (-1, 0), (0, -1)]

sage: s.slopes(relative=True)
[(0, 1), (0, 1), (0, 1), (0, 1)]

A polygon with a marked point:

sage: from flatsurf import Polygon
sage: p = Polygon(vertices=[(0, 0), (2, 0), (4, 0), (2, 2)])
sage: p.slopes()
[(2, 0), (2, 0), (-2, 2), (-2, -2)]
sage: p.slopes(relative=True)
[(-4, 4), (4, 0), (-4, 4), (0, 8)]

vector_space()

Return the vector space of dimension 2 in which this polygon embeds.

EXAMPLES:

sage: from flatsurf import Polygons
sage: C = Polygons(QQ)
sage: C.vector_space()
doctest:warning
...
UserWarning: vector_space() has been deprecated and will be removed in a future version of sage-flatsurf; use base_ring().fraction_field()**2 instead
Vector space of dimension 2 over Rational Field

vertex(i)

Return coordinates for the i-th vertex of this polygon.

EXAMPLES:

The i wraps around if it is negative or exceeds the number of vertices in this polygon:

sage: from flatsurf import polygons
sage: s = polygons.square()
sage: s.vertex(-1)
(0, 1)
sage: s.vertex(0)
(0, 0)
sage: s.vertex(1)
(1, 0)
sage: s.vertex(2)
(1, 1)
sage: s.vertex(3)
(0, 1)
sage: s.vertex(4)
(0, 0)

vertices(marked_vertices=True)

Return the vertices of this polygon in counterclockwise order as vectors in the real plane.

INPUT:

• marked_vertices – a boolean (default: True); whether to include marked vertices that are not actually corners of the polygon.

EXAMPLES:

sage: from flatsurf import polygons
sage: s = polygons.square()
sage: s.vertices()
((0, 0), (1, 0), (1, 1), (0, 1))

class Rational(base_category)

The category of rational Euclidean polygons.

Note

This category must be defined here to make SageMath’s test suite pass. Otherwise we get “The super categories of a category over base should be a category over base (or the related Bimodules) or a singleton category”; we did not investigate what exactly is going on here.

class Simple(base_category)

The subcategory of Euclidean polygons without self-intersection in the real plane.

EXAMPLES:

sage: from flatsurf.geometry.categories import EuclideanPolygons
sage: EuclideanPolygons(QQ).Simple()
Category of simple euclidean polygons over Rational Field

class Convex(base_category)

The subcategory of the simple convex Euclidean polygons.

EXAMPLES:

sage: from flatsurf.geometry.categories import EuclideanPolygons
sage: EuclideanPolygons(QQ).Simple().Convex()
Category of convex simple euclidean polygons over Rational Field

class ParentMethods

Provides methods available to all simple convex Euclidean polygons.

If you want to add functionality to all polygons, independent of implementation, you probably want to put it here.

circumscribed_circle()

Returns the circle which circumscribes this polygon. Raises a ValueError if the polygon is not circumscribed by a circle.

EXAMPLES:

sage: from flatsurf import Polygon
sage: P = Polygon(vertices=[(0,0),(1,0),(2,1),(-1,1)])
sage: P.circumscribed_circle()
Circle((1/2, 3/2), 5/2)

circumscribing_circle()

contains_point(point, translation=None)

Return whether the point is within the polygon (after the polygon is possibly translated)

find_separatrix(direction=None, start_vertex=0)

Returns a pair (v,same) where v is a vertex and same is a boolean. The provided parameter “direction” should be a non-zero vector with two entries, or by default direction=(0,1).

A separatrix is a ray leaving a vertex and entering the polygon.

The vertex v will have a separatrix leaving it which is parallel to direction. The returned value “same” answers the question if this separatrix points in the same direction as “direction”. There is a boundary case: we allow the separatrix to be an edge if and only if traveling along the sepatrix from the vertex would travel in a counter-clockwise direction about the polygon.

The vertex returned is uniquely defined from the above if the polygon is a triangle. Otherwise, we return the first vertex with this property obtained by inspecting starting at start_vertex (defaults to 0) and then moving in the counter-clockwise direction.

EXAMPLES:

sage: from flatsurf import polygons
sage: p=polygons.square()
sage: print(p.find_separatrix())
(1, True)
sage: print(p.find_separatrix(start_vertex=2))
(3, False)

flow(point, holonomy, translation=None)

Flow a point in the direction of holonomy for the length of the holonomy, or until the point leaves the polygon. Note that ValueErrors may be thrown if the point is not in the polygon, or if it is on the boundary and the holonomy does not point into the polygon.

INPUT:

• point – a point in the closure of the polygon (vector over the underlying base_ring())

• holonomy – direction and magnitude of motion (vector over the underlying base_ring())

• translation – optional translation to applied to the polygon (vector over the underlying base_ring())

OUTPUT:

• The point within the polygon where the motion stops (or leaves the polygon)

• The amount of holonomy left to flow

• a PolygonPosition object representing the combinatorial position of the stopping point

EXAMPLES:

sage: from flatsurf.geometry.polygon import polygons
sage: s = polygons.square()
sage: V = QQ**2
sage: p = V((1/2, 1/2))
sage: w = V((2, 0))
sage: s.flow(p, w)
((1, 1/2), (3/2, 0), point positioned on interior of edge 1 of polygon)

flow_map(direction)

Return a polygonal map associated to the flow in direction in this polygon.

EXAMPLES:

sage: from flatsurf.geometry.polygon import Polygon
sage: S = Polygon(vertices=[(0,0),(2,0),(2,2),(1,2),(0,2),(0,1)])
sage: S.flow_map((0,1))
 Flow polygon map:
  3 2
  0
 top lengths: [1, 1]
 bot lengths: [2]
sage: S.flow_map((1,1))
Flow polygon map:
 3 2 1
 4 5 0
top lengths: [1, 1, 2]
bot lengths: [1, 1, 2]
sage: S.flow_map((-1,-1))
Flow polygon map:
 0 5 4
 1 2 3
top lengths: [2, 1, 1]
bot lengths: [2, 1, 1]

sage: K.<sqrt2> = NumberField(x^2 - 2, embedding=AA(2).sqrt())
sage: S.flow_map((sqrt2,1))
Flow polygon map:
 3 2 1
 4 5 0
top lengths: [1, 1, 2*sqrt2]
bot lengths: [sqrt2, sqrt2, 2]

flow_to_exit(point, direction)

Flow a point in the direction of holonomy until the point leaves the polygon. Note that ValueErrors may be thrown if the point is not in the polygon, or if it is on the boundary and the holonomy does not point into the polygon.

INPUT:

• point – a point in the closure of the polygon (as a vector)

• holonomy – direction of motion (a vector of non-zero length)

OUTPUT:

• The point in the boundary of the polygon where the trajectory exits

• a PolygonPosition object representing the combinatorial position of the stopping point

is_half_translate(other, certificate=False)

Return whether other is a translate or half-translate of self.

If certificate is set to True then return also a pair (orientation, index).

EXAMPLES:

sage: from flatsurf import Polygon
sage: S = Polygon(vertices=[(0,0), (3,0), (1,1)])
sage: T1 = S.translate((2,3))
sage: S.is_half_translate(T1)
True
sage: T2 = Polygon(vertices=[(-1,1), (1,0), (2,1)])
sage: S.is_half_translate(T2)
True
sage: T3 = Polygon(vertices=[(0,0), (3,0), (2,1)])
sage: S.is_half_translate(T3)
False

sage: S.is_half_translate(T1, certificate=True)
(True, (0, 1))
sage: half_translate, cert = S.is_half_translate(T2, certificate=True)
sage: assert half_translate
sage: shift, rot = cert
sage: Polygon(edges=[rot * S.edge(k + shift) for k in range(3)]).translate(T2.vertex(0)) == T2
True
sage: S.is_half_translate(T3, certificate=True)
(False, None)

is_isometric(other, certificate=False)

Return whether self and other are isometric convex polygons via an orientation preserving isometry.

If certificate is set to True return also a pair (index, rotation) of an integer index and a matrix rotation such that the given rotation matrix identifies this polygon with the other and the edges 0 in this polygon is mapped to the edge index in the other.

EXAMPLES:

sage: from flatsurf import Polygon, polygons
sage: S = polygons.square()
sage: S.is_isometric(S)
True
sage: U = matrix(2,[0,-1,1,0]) * S
sage: U.is_isometric(S)
True

sage: x = polygen(QQ)
sage: K.<sqrt2> = NumberField(x^2 - 2, embedding=AA(2)**(1/2))
sage: S = S.change_ring(K)
sage: U = matrix(2, [sqrt2/2, -sqrt2/2, sqrt2/2, sqrt2/2]) * S
sage: U.is_isometric(S)
True

sage: U2 = Polygon(edges=[(1,0), (sqrt2/2, sqrt2/2), (-1,0), (-sqrt2/2, -sqrt2/2)])
sage: U2.is_isometric(U)
False
sage: U2.is_isometric(U, certificate=True)
(False, None)

sage: S = Polygon(edges=[(1,0), (sqrt2/2, 3), (-2,3), (-sqrt2/2+1, -6)])
sage: T = Polygon(edges=[(sqrt2/2,3), (-2,3), (-sqrt2/2+1, -6), (1,0)])
sage: isometric, cert = S.is_isometric(T, certificate=True)
sage: assert isometric
sage: shift, rot = cert
sage: Polygon(edges=[rot * S.edge((k + shift) % 4) for k in range(4)]).translate(T.vertex(0)) == T
True


sage: T = (matrix(2, [sqrt2/2, -sqrt2/2, sqrt2/2, sqrt2/2]) * S).translate((3,2))
sage: isometric, cert = S.is_isometric(T, certificate=True)
sage: assert isometric
sage: shift, rot = cert
sage: Polygon(edges=[rot * S.edge(k + shift) for k in range(4)]).translate(T.vertex(0)) == T
True

is_translate(other, certificate=False)

Return whether other is a translate of self.

EXAMPLES:

sage: from flatsurf import Polygon
sage: S = Polygon(vertices=[(0,0), (3,0), (1,1)])
sage: T1 = S.translate((2,3))
sage: S.is_translate(T1)
True
sage: T2 = Polygon(vertices=[(-1,1), (1,0), (2,1)])
sage: S.is_translate(T2)
False
sage: T3 = Polygon(vertices=[(0,0), (3,0), (2,1)])
sage: S.is_translate(T3)
False

sage: S.is_translate(T1, certificate=True)
(True, (0, 1))
sage: S.is_translate(T2, certificate=True)
(False, None)
sage: S.is_translate(T3, certificate=True)
(False, None)

j_invariant()

Return the Kenyon-Smille J-invariant of this polygon.

The base ring of the polygon must be a number field.

The output is a triple (Jxx, Jyy, Jxy) that corresponds respectively to the Sah-Arnoux-Fathi invariant of the vertical flow, the Sah-Arnoux-Fathi invariant of the horizontal flow and the \(xy\)-matrix.

EXAMPLES:

sage: from flatsurf import polygons

sage: polygons.right_triangle(1/3,1).j_invariant()
(
          [0 0]
(0), (0), [1 0]
)

The regular 8-gon:

sage: polygons.regular_ngon(8).j_invariant()
(
          [2 2]
(0), (0), [2 1]
)

(
               [  0 3/2]
(1/2), (-1/2), [3/2   0]
)

Some extra debugging:

sage: K.<a> = NumberField(x^3 - 2, embedding=AA(2)**(1/3))
sage: ux = 1 + a + a**2
sage: uy = -2/3 + a
sage: vx = 1/5 - a**2
sage: vy = a + 7/13*a**2

sage: from flatsurf import Polygon
sage: p = Polygon(edges=[(ux, uy), (vx,vy), (-ux-vx,-uy-vy)], base_ring=K)
sage: Jxx, Jyy, Jxy = p.j_invariant()

sage: from flatsurf.geometry.categories import EuclideanPolygons
sage: EuclideanPolygons.Simple.Convex.ParentMethods._wedge_product(ux.vector(), vx.vector()) == Jxx
True
sage: EuclideanPolygons.Simple.Convex.ParentMethods._wedge_product(uy.vector(), vy.vector()) == Jyy
True

subdivide()

Return a list of triangles that partition this polygon.

For each edge of the polygon one triangle is created that joins this edge to the centroid() of this polygon.

EXAMPLES:

sage: from flatsurf import polygons
sage: P = polygons.regular_ngon(3); P
Polygon(vertices=[(0, 0), (1, 0), (1/2, 1/2*a)])
sage: print(P.subdivide())
[Polygon(vertices=[(0, 0), (1, 0), (1/2, 1/6*a)]),
 Polygon(vertices=[(1, 0), (1/2, 1/2*a), (1/2, 1/6*a)]),
 Polygon(vertices=[(1/2, 1/2*a), (0, 0), (1/2, 1/6*a)])]

sage: P = polygons.regular_ngon(4)
sage: print(P.subdivide())
[Polygon(vertices=[(0, 0), (1, 0), (1/2, 1/2)]),
 Polygon(vertices=[(1, 0), (1, 1), (1/2, 1/2)]),
 Polygon(vertices=[(1, 1), (0, 1), (1/2, 1/2)]),
 Polygon(vertices=[(0, 1), (0, 0), (1/2, 1/2)])]

Sometimes alternating with subdivide_edges() can produce a more uniform subdivision:

sage: P = polygons.regular_ngon(4)
sage: print(P.subdivide_edges(2).subdivide())
[Polygon(vertices=[(0, 0), (1/2, 0), (1/2, 1/2)]),
 Polygon(vertices=[(1/2, 0), (1, 0), (1/2, 1/2)]),
 Polygon(vertices=[(1, 0), (1, 1/2), (1/2, 1/2)]),
 Polygon(vertices=[(1, 1/2), (1, 1), (1/2, 1/2)]),
 Polygon(vertices=[(1, 1), (1/2, 1), (1/2, 1/2)]),
 Polygon(vertices=[(1/2, 1), (0, 1), (1/2, 1/2)]),
 Polygon(vertices=[(0, 1), (0, 1/2), (1/2, 1/2)]),
 Polygon(vertices=[(0, 1/2), (0, 0), (1/2, 1/2)])]

subdivide_edges(parts=2)

Return a copy of this polygon whose edges have been split into parts equal parts each.

INPUT:

• parts – a positive integer (default: 2)

EXAMPLES:

sage: from flatsurf import polygons
sage: P = polygons.regular_ngon(3); P
Polygon(vertices=[(0, 0), (1, 0), (1/2, 1/2*a)])
sage: P.subdivide_edges(1) == P
True
sage: P.subdivide_edges(2)
Polygon(vertices=[(0, 0), (1/2, 0), (1, 0), (3/4, 1/4*a), (1/2, 1/2*a), (1/4, 1/4*a)])
sage: P.subdivide_edges(3)
Polygon(vertices=[(0, 0), (1/3, 0), (2/3, 0), (1, 0), (5/6, 1/6*a), (2/3, 1/3*a), (1/2, 1/2*a), (1/3, 1/3*a), (1/6, 1/6*a)])

class ParentMethods

Provides methods available to all simple Euclidean polygons.

If you want to add functionality to all polygons, independent of implementation, you probably want to put it here.

triangulate()

Return a triangulation of this polygon.

Returns a pair consisting of a surface and a bidict. The surfaces consists of the triangles that form the triangulation, glued to the original polygon. The bidict provides the mapping from the edge index of the polygon to the (label, edge) of the corresponding unglued edge in the surface.

ALGORITHM:

We use a simple quadratic time ear-clipping algorithm. There are asymptotically faster algorithms out there. But we are usually dealing with a very small number of vertices, so the asymptotic behavior does not seem to be the limiting factor here.

EXAMPLES:

We triangulate a non-convex polygon:

sage: from flatsurf import Polygon
sage: P = Polygon(vertices=[(0,0), (1,0), (1,1), (0,1), (0,2), (-1,2), (-1,1), (-2,1),
....:                    (-2,0), (-1,0), (-1,-1), (0,-1)])
sage: P.triangulate()
(Translation Surface with boundary built from 6 isosceles triangles and 4 triangles,
 bidict({0: (0, 0), 3: (2, 0), 7: (6, 0), 1: (0, 1), 2: (1, 1), 4: (2, 1), 5: (4, 1), 6: (5, 1), 8: (6, 1), 9: (8, 1), 10: (9, 1), 11: (9, 2)}))

triangulation()

Return a list of pairs of indices of vertices that together with the boundary form a triangulation.

EXAMPLES:

We triangulate a non-convex polygon:

sage: from flatsurf import Polygon
sage: P = Polygon(vertices=[(0,0), (1,0), (1,1), (0,1), (0,2), (-1,2), (-1,1), (-2,1),
....:                    (-2,0), (-1,0), (-1,-1), (0,-1)])
sage: P.triangulation()
[(0, 2), (2, 8), (3, 5), (6, 8), (8, 3), (3, 6), (9, 11), (0, 9), (2, 9)]

class SubcategoryMethods

WithAngles(angles)

Return the subcategory of polygons with fixed angles.

INPUT:

• angles – a finite sequence of numbers, the inner angles of the polygon; the angles are automatically normalized to sum to \((n-2)π\).

EXAMPLES:

sage: from flatsurf.geometry.categories import EuclideanPolygons
sage: EuclideanPolygons(AA).WithAngles([1, 2, 3])
Category of euclidean triangles with angles (1/12, 1/6, 1/4) over Algebraic Real Field

module()

Return the free module of rank 2 in which these polygons embed.

EXAMPLES:

sage: from flatsurf import Polygons
sage: C = Polygons(QQ)
sage: C.module()
doctest:warning
...
UserWarning: module() has been deprecated and will be removed in a future version of sage-flatsurf; use base_ring()**2 instead
Vector space of dimension 2 over Rational Field

sage: from flatsurf import EuclideanPolygonsWithAngles
sage: C = EuclideanPolygonsWithAngles(1, 2, 3)
sage: C.module()
Vector space of dimension 2 over Number Field in c with defining polynomial x^2 - 3 with c = 1.732050807568878?

vector_space()

Return the vector space of dimension 2 in which these polygons embed.

EXAMPLES:

sage: from flatsurf import Polygons
sage: C = Polygons(QQ)
sage: C.vector_space()
Vector space of dimension 2 over Rational Field

sage: from flatsurf import EuclideanPolygonsWithAngles
sage: C = EuclideanPolygonsWithAngles(1, 2, 3)
sage: C.vector_space()
doctest:warning
...
UserWarning: vector_space() has been deprecated and will be removed in a future version of sage-flatsurf; use base_ring().fraction_field()**2 instead
Vector space of dimension 2 over Number Field in c with defining polynomial x^2 - 3 with c = 1.732050807568878?

super_categories()

Return the categories Euclidean polygons are also contained in, namely the polygons.

EXAMPLES:

sage: from flatsurf.geometry.categories import EuclideanPolygons
sage: EuclideanPolygons(QQ).super_categories()
[Category of polygons over Rational Field]